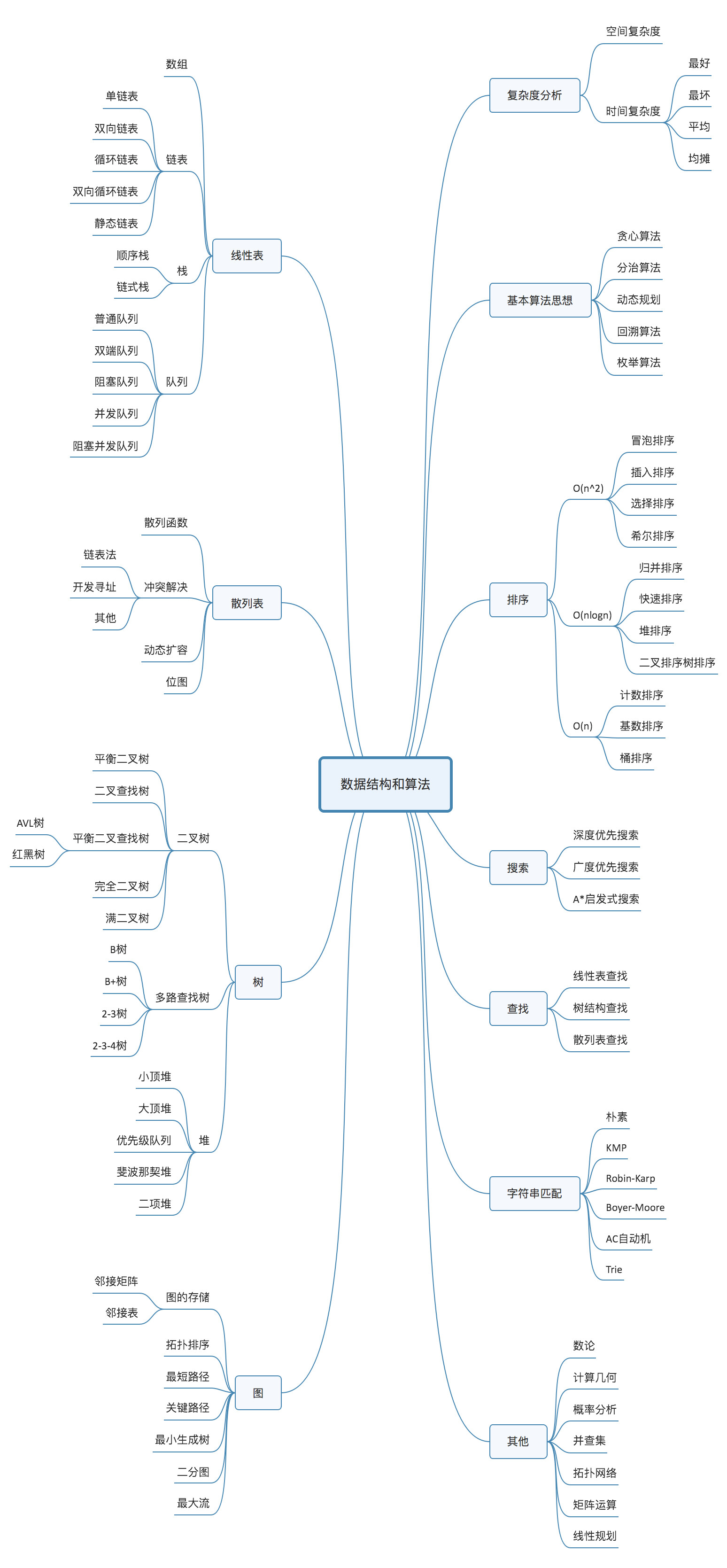
7.5 数据结构与算法

数据结构

Java数据结构

• List
  • LinkedList, 链表实现
  • Vector, 数组实现, 读写安全, 通过synchronized实现
• 栈(Stack)
• Set
  • LinkedHashSet
  • HashSet, 使用HashMap实现
• 二叉树
  • 满二叉树, 除了叶子节点, 其它节点均有两个子节点
  • 完全二叉树, 叶子结点只可能在层次最大的两层出现且前k-1层的结点是”满”的, 第k层的结点集中在左边
  • 二叉树的遍历
    • 先序遍历, 根结点 -> 左子树 -> 右子树; 例子结果: 1 2 4 5 7 8 3 6
    • 中序遍历, 左子树 -> 根结点 -> 右子树; 例子结果: 4 2 7 5 8 1 3 6
    • 后序遍历, 左子树 -> 右子树 -> 根结点; 例子结果: 4 7 8 5 2 6 3 1
    • 层次遍历, 按层次遍历; 例子结果: 1 2 3 4 5 6 7 8
  • 二叉平衡树（AVL树）, 即左右子树高度差不超过1（高度平衡, 频繁插入和删除, 会引起频繁的rebalance, 导致效率下降）
    • 旋转(失去平衡包含左左, 右右, 左右, 右左四种情况)
      • 左左型

        public AVLNode<K,V> rotateLL(AVLNode<K,V> node) {
            // 把node的left结点作为根结点
            var top = node.left
            // 截断原来的node.left, 并把top结点(新的根结点)的右子结点作为node.left结点
            node.left = top.right;
            // 原来的根结点(node)作为top结点的右结点
            top.right = node;
            // 重新结算高度
            node.height = Math.Max(Height(node.left, Height(node.right)) + 1;
            top.height = Math.Max(Height(top.left), Height(top.right)) + 1;
            return top;
        }
        

      • 右右型

        public AVLNode<K,V> rotateRR(AVLNode<K,V> node) {
            // 类似rotateLL, 不多解释
            var top = node.right;
            node.right = top.left;
            top.left = node;
            // 重新结算高度
            ...
            return top;
        }
        

      • 左右型

        public AVLNode<K,V> rotateLR(AVLNode<K,V> node) {
            // 先右右旋转
            node.left = rotateRR(node.left);
            // 再左左旋转
            return rotateLL(node);
        }
        

      • 右左型

        public AVLNode<K,V> rotateRL(AVLNode<K,V> node) {
          // 先左左旋转
          node.right = rotateLL(node.right);
          // 再右右旋转
          return rotateRR(node);
        }
        

    • 插入

      public AVLNode<K,V> add(K key, V value, AVLNode<K, V> tree) {
        if (tree == null) {
          tree = new AVLNode<K, V>(key, value, null, null);
        }
        if (key.CompareTo(tree.key) < 0) {
          // 找到不断往左遍历, 找到可插入点
          tree.left = add(key, value, tree.left);
          if (Height(tree.left) - Height(tree.right) == 2) {
            // 左左型, key小于tree.left.key, 说明key放到tree.left的左边
            if (key.CompareTo(tree.left.key) < 0) {
                tree = rotateLL(tree);
            } else {
                tree = rotateLR(tree);
            }
          }
        }
        if (key.CompareTo(tree.key) > 0) {
          tree.right = add(key, value, tree.right);
          if (Height(tree.right) - Height(tree.left) == 2) {
            if (key.CompareTo(tree.right.key) > 0) {
                tree = rotateRR(tree);
            } else {
                tree = rotateRL(tree);
            }
          }
        }
      
        if (key.CompareTo(tree.key) == 0) {
          tree.attach.add(value);
        }
      
        //计算高度
        tree.height = Math.Max(Height(tree.left), Height(tree.right)) + 1;
      
        return tree;
      }
      

• 红黑树 (非高度平衡, 插入最多旋转2次, 删除旋转3次)
  • 特性
    1. 结点要么红要么黑
    2. 根结点是黑的
    3. 每个叶子结点(叶结点即树尾端NIL指针)都是黑的
    4. 如果一个结点是红的, 它的两个子结点均是黑的
    5. 对于任意结点, 到叶子结点的路径包含相同数量的黑结点

  • 左旋

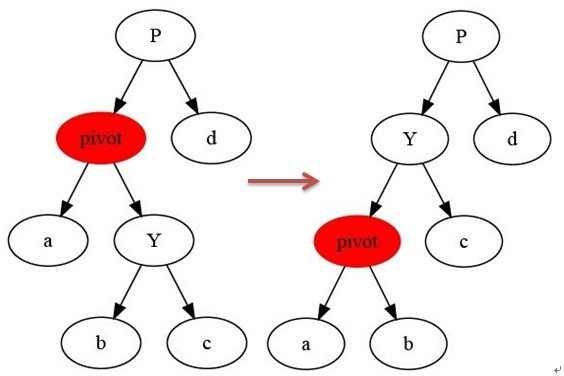
      LeftRoate(T, x)
       y <- x.right;
       x.right <- y.left;
       if(y.left != Nil)
        y.left.parent <- x;
       y.parent <- x.parent;
       if x.parent == Nil
        then T.root <- y;
       else if x == x.parent.left
        then x.parent.left <- y;
       else x.parent.right <- y;
       y.left <- x;
       x.parent <- y;  
    

  • 右旋

    RightRoate(T, x)
    y <- x.left;
    x.left <- y.right;
    if(y.right != Nil)
      y.right.parent <- x;
    y.parent <- x.parent;
    if x.parent == Nil
      then T.root <- y
    else if x == x.parent.right
      then x.parent.right <- y;
    else x.parent.left <- y;
    y.right <- x;
    x.parent <- y;
    

  • 插入

  • 删除
• 堆
  • 符合安全二叉树且父结点比子结点大（或小）, 根结点最大的堆则叫做最大堆，根节点最小的堆则叫做最小堆
• B树
  • B+树
  • B*树

算法

排序算法

• 冒泡排序 O(N^2)

  public void bubbleSort(int[] nums) {
    if(nums == null) {
      return ;
    }
    for(int i = 0; i < nums.length; i++) {
      for(int j = 0; j < nums.length - 1 - i; j++) {
        if(nums[j] > nums[j + 1]) {
          int tmp = nums[j];
          nums[j]  = nums[j + 1];
          nums[j + 1] = tmp;
        }
      }
    }
  }

• 插入排序 O(N^2), 平均情况下插入排序需要n*(n-1)/4

  public void insertSort(int[] nums) {
    if(nums == null) {
      return ;
    }
    for (int i = 0; i < nums.length; i++) {
      int temp = nums[i];
      int j = i - 1;
      while (j >= 0 && nums[j] > temp) {
        nums[j + 1] = nums[j];
        j--;
      }
      nums[j+1] = temp;
    }
  }

• 选择排序 O(N^2), 平均情况下选择排序需要n*(n-1)/2

  public void selectionSort(int[] nums) {
    if(nums == null) {
      return ;
    }
    for (int i = 0; i < nums.length; i++) {
      int minNum = nums[i];
      int minIndex = 0;
      for (int j = 0; j < nums.length; j++) {
        if(nums[j] < minNum) {
          minNum = nums[j];
          minIndex = j;
        }
      }
      int temp = nums[i];
      nums[i] = minNum;
      nums[minIndex] = temp;
    }
  }

• 快速排序（O(nlg(n))）

  public void quickSort(int nums[], int low, int high) {
    if(low < hight) {
        int partition = partition(nums, low, high);
        quickSort(nums, low, partition - 1);
        quickSort(nums, partition + 1, high);
    }
  }

  public int partition(int nums[], int low, int high) {
    int pivot = nums[low];
    while (low < high) {
      while (low < high && nums[high] > pivot) {
        high--;
      }
      nums[low] = nums[high];
      while (low < high && nums[low] <= pivot) {
        low++;
      }
      nums[high] = nums[low];
    }
    num[low] = pivot;
    return low;
  }

• 归并排序（O(nlg(n))）

  public void mergeSort(int nums[], int left, int right, temp[]) {
    if (left < right) {
      int mid = (left + right)/2;
      mergeSort(nums, left, mid, temp);
      mergeSort(nums, mid + 1, right, temp);
      merge(nums, left, mid, right, temp);
    }
  }

  public void merge(int nums[], int left, int mid, int right, int temp[]) {
    int i = left;
    int j = mid + 1;
    int t = 0;
    while (i <= mid && j <= right) {
      if (arr[i] <= arr[j]) {
        temp[t++] = arr[i++];
      } else {
        temp[t++] = arr[j++];
      }
    }
    while (i <= mid) {
      temp[t++] = arr[i++];
    }
    while (j <= right) {
      temp[t++] = arr[j++];
    }
    t = 0;
    while(left <= right) {
      arr[left++] = temp[t++];
    }
  }

• 堆排序（O(nlg(n))）

// parent = (child - 1) / 2
// leftChild = parent * 2 + 1; rightChild = parent * 2 + 2;
public void heapSort(int nums[]) {
  // 1. 构建最大/最小堆
  int len = nums.length;
  buildHeap(nums, len);

  // 根结点和最后的叶子结点交换, 并不断继续构建堆, 再交换, 最终得出来有序数组
  for (int i = len - 1; i >= 0; i--) {
    // 叶子结点和根结点交换
    swap(nums, i, 0);
    heapify(nums, i, 0);
  }

}

private void swap(int nums[], int i, int j) {
  int temp = nums[i];
  nums[i] = nums[j];
  nums[j] = temp;
}

private void buildHeap(int nums[], int len) {
  int parentOfLastLeaf = (len - 1) / 2;
  // 从最后叶子结点的父结点开始堆化, 构建堆
  for (int i = parentOfLastLeaf; i >= 0; i--) {
    heapify(nums, len, i);
  }
}

private void heapify(int nums[], int len, int i) {
  if (i >= len) return;
  int leftChild = 2 * i + 1;
  int rightChild = 2 * i + 2;
  int max = i;
  if (leftChild < len && nums[leftChild] > nums[max]) {
    max = leftChild;
  }
  if (rightChild < len && nums[rightChild] > nums[max]) {
    max = rightChild;
  }
  if (max != i) {
      swap(nums, max, i);
      heapify(num, len, max);
  }
}

查找算法

• 顺序查找（适合）

public int search(int nums[], int targetNumber) {
  int targetIndex = -1;
  for (int i = 0; i < nums.length ; i++) {
    if (nums[i] == targetNumber) {
      targetIndex = i;
      break;
    }
  }
  return targetIndex;
}

• 二分查找

public int binarySearch(int[] array, int searchKey) {
  int low = 0;
  int high = array.length;
  while (low <= high) {
    int mid = (low + high) / 2;
    if (searchKey == array[mid]) {
      return mid;
    } else if (searchKey > array[mid]) {
      low = mid + 1;
    } else {
      high = mid - 1；
    }
  }
  return -1;
}

• 插值查找
• 斐波那契查找

基本算法思想

• 贪心算法, 基本思想, 把问题拆解成N个小问题, 再根据小问题取最优解, 即局部最优解; 缺点: 1. 不能保证全局最优, 2. 不能求解最大或最小解问题
• 分治算法, 基本思想, 把复杂问题分成两个或多个相似的子问题, 直到最后子问题可以简单求解, 元问题的解即子问题的解的合并, 经典问题场景: 二分搜索, 快排, 归并排序等, 包含以下特征:
  1. 问题的规模缩小到一定程度可以容易解决
  2. 问题可以分解为若干小问题, 即该问题具有最优子结构性质
  3. 分解的子问题的解可以合并为该问题的解(能否使用分治算法的关键)
  4. 分解的子问题互相独立, 即子问题之间不包含公共的子子问题
• 动态规划（将一个问题拆成多个子问题, 分别求解这些子问题, 即可推断大问题的解）
  • 无后性, 即给定某一阶段的状态, 则这一阶段的状态以后的过程不受以前状态的影响
  • 最优子结构, 即大问题的最优解可以由小问题的最优解推出
  • 重复子问题
  • 解决思路
    • 状态转移表法, 一般动态规划解决的问题都可以用回溯算法的暴力搜索解决, 即可用回溯算法解决, 定义状态, 每个状态即一个结点, 画出递归树, 从递归树看是否存在重复子问题, 子问题如何产生, 以此寻找规律, 最后决定是否使用动态规划
    • 状态转移方程法, 写出递归公式, 即状态转移方程, 一般情况下, 1). 递归加”备忘录”, 2). 迭代递归
    • 设计, 对于状态x, 记我们要求出的答案(e.g.最小费用)为f(x), 我们的目标是f(T), 找出f(x)与哪些局面有关(记为P), 写出一个式子(称为状态转移方程), 通过f(p)来推倒(fx)
    • 动态规划三连, 即我是谁？->设计状态, 表示局面, 我从哪里来?, 我要到哪里去? -> 设计转移
• 回溯算法, 基本思想, 按照深度优先搜索的策略, 从根结点出发深度探索解空间树, 当探索到结点时, 先判断该结点是否包含问题的解, 如果包含就从该结点继续往下探索, 否则将逐层向其祖先结点回溯。

• 枚举算法, 基本思想, 把问题一一列举, 答案合适则保留, 否则舍弃

• TopK算法, 基本思想是堆排序, 根据K限定对堆进行增加删除
• 滑动窗口, 解决数组/字符串的子元素的问题, 解决嵌套循环, 转换为单循环问题, 降低复杂度, 可以解决查找最大/最小k子阵列，XOR，乘积，求和等问题
  • 最长连续递增序列
  • 无重复字符的最长子串
  • 最小覆盖子串
• KMP算法, 基本思想寻找字符串第i个字符与和模式串串的前缀/后缀集合交集的最大元素的长度, 即部分匹配表(Partial Match Table)数组. 易懂教程

public int kmpSearch(String originString, String matchString) {
  int i = 0;
  int j = 0;
  int next[] = getNext(originString, matchString);
  while (i < originString.length() && j < matchString.length()) {
    if (j == -1 || originString.indexOf(i).equals(matchString.indexOf(j))) {
      i++;
      j++;
    } else {
      j = next[i];
    }
  }

  if (j > 0) {
    return i - j;
  } else {
    return -1;
  }
}

public int[] getNext(String originString, String matchString) {
  int[] next = new int[originString.length()];
  next[0] = -1;
  int i = 0;
  int j = -1;
  while (i < originString.length) {
    if (j == -1 || originString.indexOf(i).equals(matchString.indexOf(j))) {
      i++;
      j++;
      next[i] = j;
    } else {
      j = next[j];
    }
  }
  return next;
}

算法知识表

习题

• 两数之和
• 求众数
• 无重复字符的最长子串
• 颠倒二进制位

参考

• 七大查找算法
• 什么是动态规划？动态规划的意义是什么？
• 系统高效地学习数据结构与算法
• 每个程序员都应该收藏的算法复杂度速查表
• Java阻塞队列ArrayBlockingQueue和LinkedBlockingQueue实现原理分析
• 红黑树深入剖析及Java实现
• 6天通吃树结构—— 第二天 平衡二叉树
• 图解排序算法(三)之堆排序
• 如何更好的理解和掌握 KMP 算法, 参考(海纳)写的答案
• 教你初步了解红黑树